Do there exist irrational numbers a and b such that a raised to the power b (aᵇ) is a rational number?
George hid the middle of this sequence:
1000 1 ? ? 50 2.718
But Cicero mentioned that the same number is missing twice.
What is the number?
P, Q, R, S and T are the digits 1, 2, 3, 4 and 5 in some order. ‘PRT’ and ‘QRS’ are both three-digit primes. Which digit is R?
The hikers can proceed as follows:
All three hikers successfully cross the river using this strategy while respecting the boat's 100 kg weight limit.
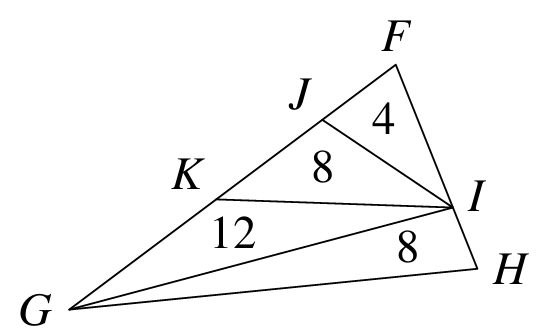
As shown in the diagram, triangle FGH is divided into four smaller triangles which have areas 4, 8, 12 and 8 respectively.What is the area of triangle IKH?
Alex is climbing a staircase with 10 steps. With each move, he can go up either 1 step or 2 steps. In how many different ways can Alex reach the top of the staircase?
When coming down the same staircase, Alex is allowed to jump over any number of steps — he may even jump directly from the top to the ground in one go.How many different ways can Alex jump down the staircase?
Is it possible to cut an 8×8 square without two diagonally opposite corners into 1×2 rectangles?

Write down a random two-digit number. What is the probability that the sum of its digits is equal to 5?
Remove 5 matchsticks to get 3 squares. Make sure that once you remove the matchsticks, there are no dangling ones remaining.

Some of the digits in the following correct addition have been replaced by the letters P, Q, R, and S, as shown. What is the value of P + Q + R + S?

My 24-hour digital clock displays hours and minutes only. How many displayed times in a 24-hour period contain at least one occurrence of the digit 5?
Find all prime numbers p for which the number p2+11 has exactly 6 different divisors (including 1 and the number itself).
In the center of a square field, a hare sits, surrounded by four wolves positioned at each corner.
The hare can move freely within the field, while the wolves can only move along the sides of the square.
Given that the maximum speed of each wolf is at most 1.4 times the maximum speed of the hare, is it possible for the hare to escape the square without being caught by the wolves?
A piece fell out of a book, where the first page is numbered 439 and the last page is numbered with the same digits in a different order. Determine the number of pages in the missing piece.
For every natural number n, prove that the expression n5 - 5n3 + 4n is always divisible by 120.
A semicircle is inscribed in a quarter circle as shown. What fraction of the quarter circle is shaded?

Given a circle with radius 1 and 100 points marked along its circumference. Prove that there exists at least one point on the circle such that the sum of the distances from this point to all 100 marked points is at least 100.
PT is the tangent to a circle O, and PB is the angle bisector of the angle TPA (see diagram). How big is the angle TBP?

Punam puts counters onto some of the cells of a 5 × 5 board.
She can put more than one counter on each cell, and she can leave some cells empty.
She tells Quinn how many counters there are in each row and column. These ten numbers are all different.
Can Quinn always work out which cells, if any, are empty?
Seven standard dice are glued together to make the solid shown.
The pairs of faces of the dice that are glued together have the same number of dots on them.
How many dots are on the surface of the solid?

A positive integer is called friendly if it is divisible by the sum of its digits.
For example, 111 is friendly but 123 is not.
Find the number of all two-digit friendly numbers.
Arrange the digits 1 to 9 in a row so that each pair of consecutive numbers forms a two-digit number divisible by either 7 or 13.
Each number from 1 to 9 should appear exactly once.
A student made an error while multiplying two three-digit numbers. Instead of noticing the multiplication sign between them, the student wrote the numbers together, forming a six-digit number.
Surprisingly, this mistake resulted in a product that was three times greater than the actual product of the two numbers.
Can you find these two original three-digit numbers?
In many parts of the world, including the USA and Europe, dates are written differently. In the USA, it's customary to write the month first, followed by the day and year (MM/DD/YYYY), while in Europe, it's common to write the day first, followed by the month and year (DD/MM/YYYY). This can sometimes lead to ambiguity, where a date could be interpreted differently depending on the format used.
How many days in a year have dates that cannot be interpreted unambiguously without knowing the specific date format being used?

This course guides you through the fundamentals of Python programming using an interactive Python library known as Turtle.

This course encompasses a range of Geometry topics such as coordinate and spatial geometry, introductory trigonometry, angles, parallel lines, congruent and similar triangles, polygons, circles, the Pythagorean Theorem, and more. Emphasis will be placed on reinforcing Algebra skills and enhancing critical thinking through problem-solving in both mathematical and real-world contexts.

Ask about our courses and offerings, and we will help you choose what works best for you.